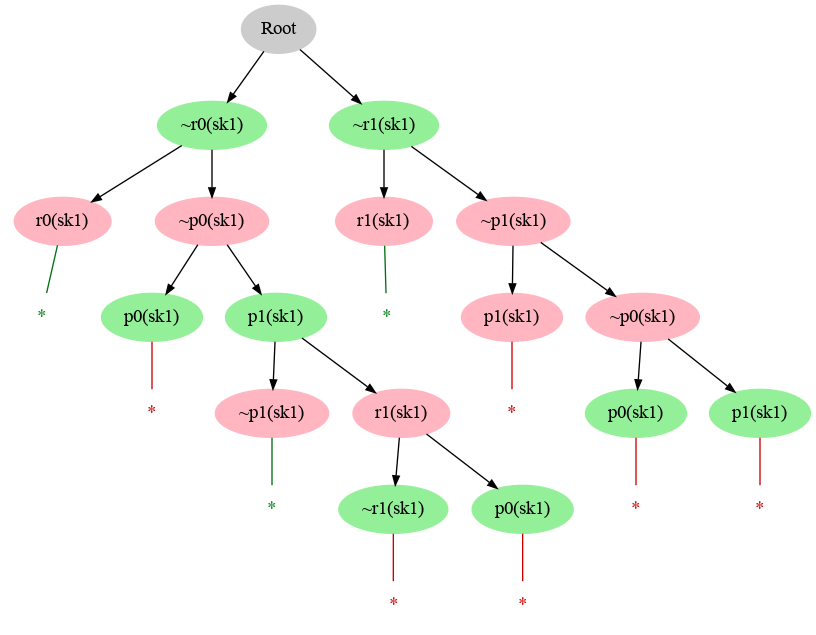
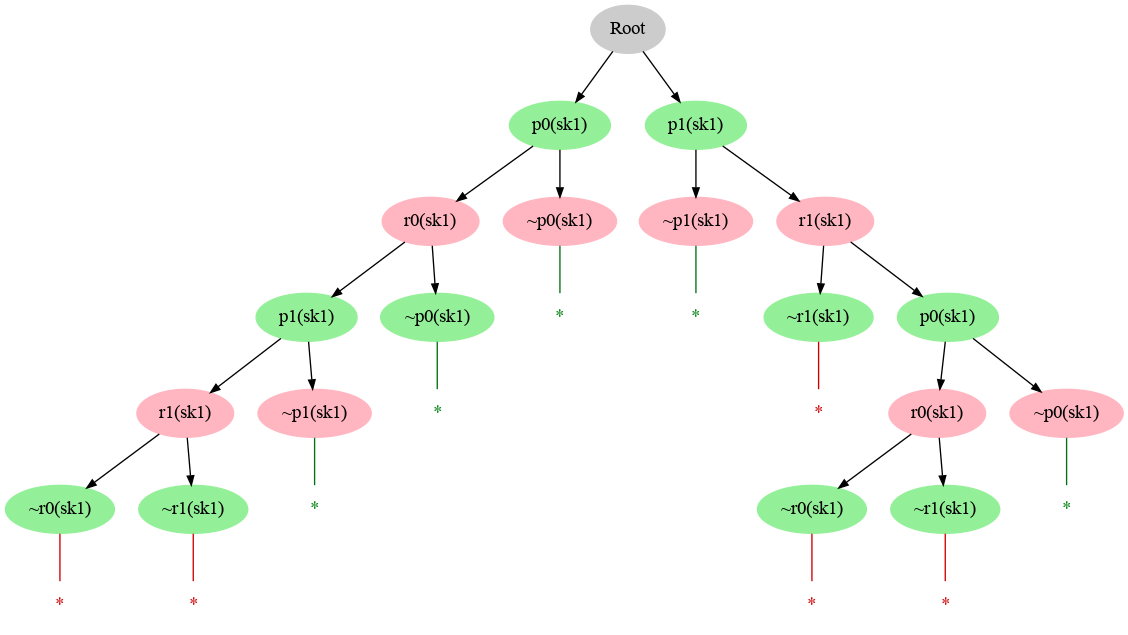
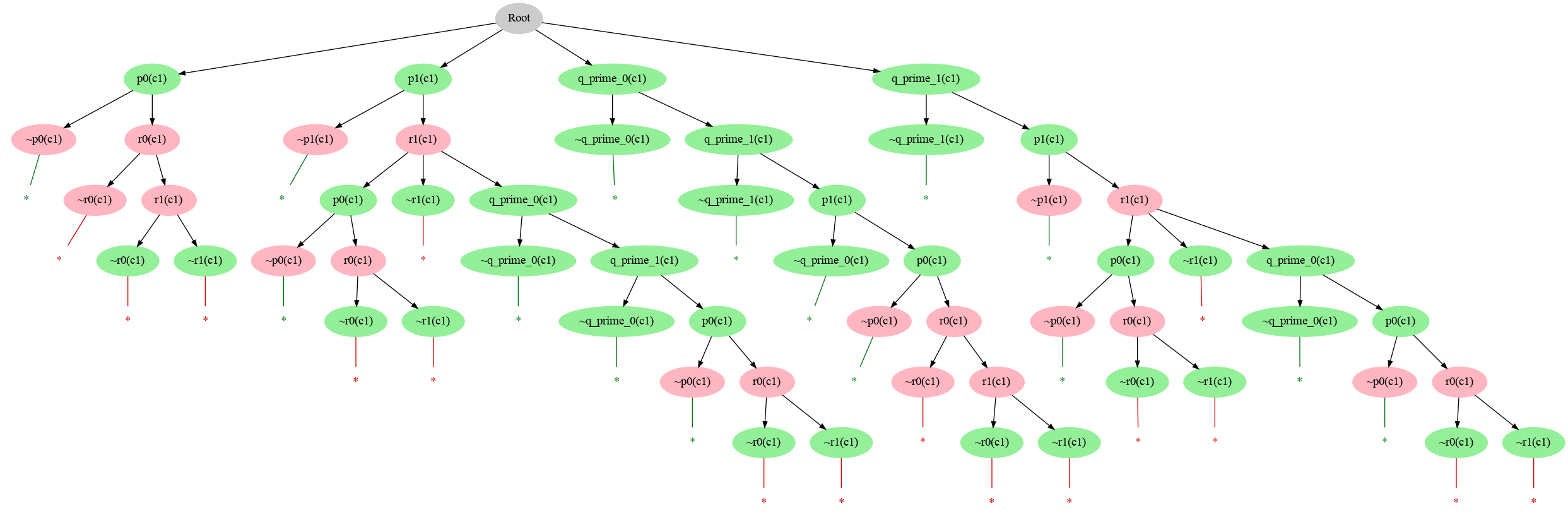
Some Two-Sided Clausal Tableaux

The following images show two-sided clausal tableaux proofs underlying interpolation for a simple synthesis problem, obtained by different provers or prover configurations.

Input: Two Programs and a Vocabulary

P = [(p(X) <-- q(X))],
Q = [(r(X) <-- p(X)),
     (r(X) <-- q(X))],
V = [p, r].

Output: The Synthesized Program

R = [(r(A)<--p(A))]

Input of the Underlying Craig-Lyndon Interpolation, as Implication

all(x, ((~q0(x);p0(x)),
        (~q1(x);p1(x)),
        (~p0(x);r0(x)),
        (~p1(x);r1(x)),
        (~q0(x);r0(x)),
        (~q1(x);r1(x)))),
all(x, ((~p0(x);p1(x)),(~q0(x);q1(x)),(~r0(x);r1(x))))

->

(ex(x, (p0(x),~p1(x);
        q_prime_0(x),~q_prime_1(x);
        r0(x),~r1(x)));
 ex(x, (q_prime_0(x),~p0(x);q_prime_1(x),~p1(x)));
 all(x, ((~p0(x);r0(x)),
         (~p1(x);r1(x)),
         (~q_prime_0(x);r0(x)),
         (~q_prime_1(x);r1(x)))))

Some Clausal Tableaux Proofs of the Implication Underlying Interpolation

Proof by CMProver, hyper form — Proof by CMProver, transformed to *hyper* form.

Converted proof by Prover9. — Resolution proof by Prover9, converted to a clausal tableau with the *hyper* property.

Contact: info@christophwernhard.com